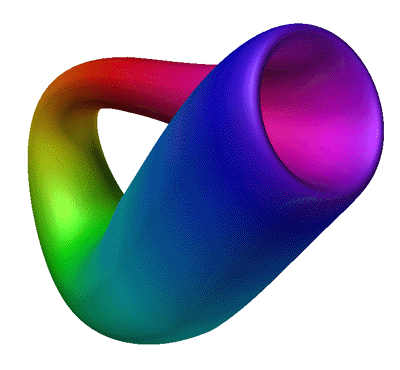Прогулки фантазеров

Опубликовано в журнале Hard'n'Soft №7 2003

От всей души я желал бы издания закона, которым обязывал бы каждого путешественника перед получением им разрешения на опубликование книг о своих путешествиях давать перед лордом верховным канцлером клятву, что все, что он собирается печатать, - безусловная истина. Тогда бы никто не вводил в обман доверчивую публику, как это делают некоторые писатели. Желая придать своим сочинениям побольше занимательности, они угощают читателя самыми грубыми вымыслами.
Джонатан Свифт. Путешествия Гулливера.

За годы разработок программ для станков с ЧПУ приходилось сталкиваться с разными поверхностями - бочкообразными, коническими, лопастями крыльчаток, винтовыми канавками, идущими одновременно в двух направлениях, ребрами, закрученными самым мудреным способом, зубцами, торчащими в пространстве бог знает как. Но это все были поверхности реальные, их можно было пощупать после изготовления. Куда интереснее поверхности не реальные, существующие лишь в виде математических моделей. Предлагаю вместе прогуляться по разным экзотическим закоулкам пространства, лабиринтам и необычным поверхностям. Вам понадобится лишь немного свободного времени, любопытство и способность морщить лоб при попытке сосредоточиться. И, конечно, шляпа для путешествий.

Шляпа для путешествий

Шляпа вылезла на середину комнаты и остановилась. Ребята смотрят на неё и трясутся от страха. Тут шляпа повернулась и поползла к дивану.
Н.Носов. Живая шляпа.

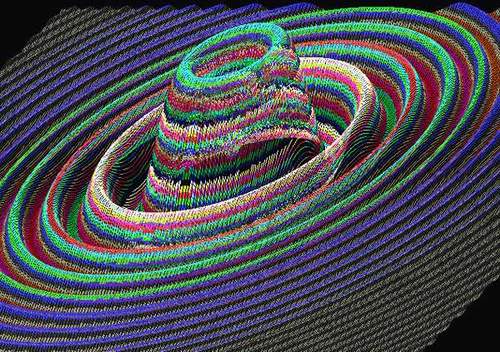
Мы сейчас не только построим шляпу, но и полюбуемся ею, примеряя для следующих путешествий. Давным-давно попалась на глаза красивая функция: Z= Sin(X²+Y²) / (X²+Y²)
Полюбуемся ею вместе:
- трёхмерная поверхность
- синус должен дать «волны»
- должна быть некоторая «горбушка»
- убывает при удалении от начала координат каким-то образом
- симметрия относительно осей
Так и просится пощупать её на экране. А вот и вариант исполнения задумки:

PROGRAM SHLAPA; USES GRAPH,DOS,CRT; VAR X,X1,Y,Y1,M,N : INTEGER; Q,W,U,Z: REAL; C: CHAR; procedure GrInit; { инициализация режима графики } var GraphDriver : Integer; { для графического адаптера } GraphMode : Integer; { для графического режима } ErrorCode : Integer; { для кода ошибки } begin GraphDriver:= Detect; { режим автоопределения } InitGraph(GraphDriver,GraphMode,''); { инициализация} ErrorCode:=GraphResult; { результат инициализации } if ErrorCode <> grOk then { если не успешно, то ...} begin Writeln('Ошибка графики:',GraphErrorMsg(ErrorCode)); Writeln('Программа остановлена.'); Halt (1) end {if} end; BEGIN GRINIT; X1:=0 ; Y1:=0 ; Q:=-15; REPEAT W:=-10; REPEAT U:=0.4*Q*Q+0.2*W*W; {1} Z:=(9*SIN(U) / (U+1))+5.3; {2} X:=TRUNC(300+27*(Q-W*COS(PI/4))); {3} Y:=TRUNC(350+27*(W*SIN(PI/4)-Z)); {4} IF W>-10 THEN LINE(X,Y,X1,Y1); {Для отсекания линий возврата в начале цикла} X1:=X ; Y1:=Y; W:=W+0.1 ; {5} SETCOLOR(TRUNC(Z*7+0)); {6} UNTIL W>13 ; Q:=Q+0.1 ; {7} UNTIL Q>18; C:=READKEY; END.

Так вот: это и есть та самая шляпа с полями, вынесенная в заголовок. Причём на экран она выходит в аксонометрии, а угол наклона локальных осей шляпы относительно экранных можно попробовать поменять в строках {3} и {4} . Самые отчаянные могут попробовать разные значения углов для проекций на X и на Y , но от такой наглости трудно ожидать прогнозируемый результат. Гораздо интереснее поиграть коэффициентами : Z= A * Sin( U ) /( U + B), где U = C * X² + D * Y² + E * X * Y
A - делает шляпу острее или положе B - ещё и сдвигает её вдоль оси Z C и D - сжимают шляпу вдоль осей X,Y E - сжимает шляпу вдоль оси, проходящей под углом 45 градусов к осям XY Для тех, у кого две макушки, интересна замена: U =( X - F ) * (X + F ) + Y². В результате шляпа раздваивается, разъезжается по оси X на величину 2*F . Аналогично можно раздвинуть шляпу и по Y : U = ( X - F ) * ( X + F ) + ( Y - G ) * ( Y + G ) получив четырёх холмистую шляпу для рогатых мутантов. Можно ещё поменять знак: U = X² - Y² , превратив шляпу в нечто гиперболическое, на шляпу не похожее, в обиходе не встречающееся . Шляпа рисуется ломаными линиями, с параметрами Q и W (локальными осями X и Y шляпы). Плавность линий зависит от величины приращений W , а частота линий от величины приращений Q . Чем меньше эти величины приращений, тем ярче шляпа, но дольше рисуется. А вы оценили раскраску шляпы? Цвет зависит от величины Z, то есть от высоты гребня (строка {6}), меняя параметры можно получать пояски на тулье и на полях и даже волнистую шахматную доску.

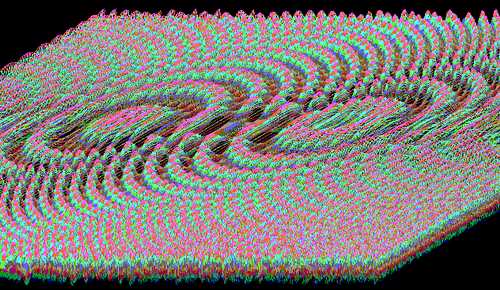
Для самых занудных и въедливых читателей, которые захотят убедиться во всем лично, предлагаем попробовать поменять Sin(U) на Sin²(U), на Cos(U), на Sin(2*U), - и вы будете вознаграждены открывшимися пейзажами - вокруг островка шляпы вдруг появляются лунные кратеры от гармоник высших порядков, объяснить которые с точки зрения тригонометрии и материализма невозможно. А ещё можно попробовать поменять . . . но не будем лишать вас удовольствия самим поиграть и насладиться своим результатом . Шляпа хранит много приятных мгновений общения с ПК , достаньте их из неё. И всё-таки невозможно удержаться, намекну: нарисуйте шляпу в полярных координатах - не пожалеете. А если центр этих координат не совпадает с центром шляпы . . . Всё - движемся дальше.

Числовой лабиринт

АЭРОСАНИ - тоже неплохое. На них меня жевали шесть часов от Ачинска. Этот дизель ревел, как твой клон-файтер. Мы неслись по очень белому снегу. "Восток-Сибирь большая", - как говорит Фань Мо.
В. Сорокин. Голубое сало.

Составление различных лабиринтов и прохождение их представляет собой прекрасную тему для тех, кто любит программировать. Лабиринтов и лабиринтоподобных игр существует очень много, представим простейший вариант для любителей самим программировать всякие математические забавы. А именно - предлагаю написать программу для числового лабиринта. Он представляет собой прямоугольную область, разбитую на квадратики, в каждом квадратике находится число. Вход в левом верхнем квадратике. При движении мы суммируем числа проходимых квадратиков. Задача состоит в том, чтобы при выходе из лабиринта в нижнем правом квадратике сумма пройденных чисел равнялась нулю. Правила условны, точки входа и выхода и конечное число можете запрограммировать по своему усмотрению. В прилагаемой программе на Turbo Pascal'e поле задано размером 10х10, а числа в ячейках от -20 до 20. Управление осуществляется клавишами со стрелками. Текущий квадратик окрашен в розовый цвет. Зона замкнута по вертикали и по горизонтали, то есть, уйдя за правую границу, мы окажемся слева. Внизу экрана выводится текущая сумма. Текст программы:

PROGRAM Labirint; USES CRT,GRAPH,DOS; VAR SUMMA,M,S,X,Y,XX,YY,I,J : INTEGER; Q : ARRAY [1..10,1..10] OF STRING ; N : ARRAY [1..10,1..10] OF INTEGER ; CH,CH1,SUMSTROKA: STRING; GraphDriver,GraphMode:INTEGER ; BEGIN RANDOMIZE ; SUMMA:=0 ; FOR I:=1 TO 10 DO FOR J:=1 TO 10 DO BEGIN N[I,J]:=20-RANDOM(40) ; STR(N[I,J],Q[I,J]); END ; GraphDriver:= Detect; режим автоопределения InitGraph(GraphDriver,GraphMode,''); инициализация SETLINESTYLE(0,0,1); XX:=1 ; YY:=1 ; SETFILLSTYLE(1,0) ; BAR(0,0,640,480) ; SETFILLSTYLE(1,7) ; setcolor(15); settextstyle(0,0,1) ; OUTTEXTXY(100,10,'Придите к правому нижнему квaдрату с суммой равной нулю.'); outtextxy(200,460,'Сумма = ') ; XX:=1 ; YY:=1 ; REPEAT Y:=40 ; M:=40 ; S:=1 ; SETFILLSTYLE(1,0) ; BAR(300,440,600,480) ; FOR I:=1 TO 10 DO FOR J:=1 TO 10 DO BEGIN SETFILLSTYLE(1,3) ; IF (I=XX) AND (J=YY) THEN SETFILLSTYLE(1,5) ; BAR(120+(I-1)*M+S,40+(J-1)*M+S,120+I*M-S,40+J*M-S) ; SETTEXTSTYLE(1,0,2) ; outtextxy(118+(I-1)*M+S+5,40+(J-1)*M+S+5,Q[I,J]); END ; SUMMA:=SUMMA+N[XX,YY] ; STR(SUMMA , SUMSTROKA) ; OUTTEXTXY(300,450,SUMSTROKA) ; ch1:=readkey; if ch1=#27 then EXIT; if ch1=#0 then ch:=readkey; if ch='K' then XX:=XX-1; if XX<1 then XX:=XX+10 ; if ch='M' then XX:=XX+1; if XX>10 then XX:=XX-10 ; if ch='H' then YY:=YY-1; if YY<1 then YY:=YY+10 ; if ch='P' then YY:=YY+1; if YY>10 then YY:=YY-10 ; UNTIL CH=#27 ; CLOSEGRAPH; END.

Опыт игры с числовым лабиринтом показывает, что основной подбор суммы начинается около выхода и сам маршрут мало влияет на результат. Особенно удобно иметь около выхода квадратики с числами +1 и -1, ходя по ним туда-сюда можно подгонять сумму к нужному значению. Программа проста и должна быть понятна любителям Паскаля. В то же время она открывает простор для творчества - можно, например, раскрасить квадратики в зависимости от их числа, установить преграды, ловушки, установить сумму для выхода в некоторых пределах, и прочие штучки. Поиграйте - навыки хождения по полям нам еще пригодятся.

Прогулки по ленте Мебиуса.

- Слушай, Том, дай мне побелить немножко!
Том задумался и сначала как будто готов был согласиться, а потом передумал: - Нет, Бен, все равно ничего не выйдет. Тетя Полли прямо трясется над этим забором. Если бы это была та сторона, что во двор, она бы слова не сказала, да и я тоже. Она прямо трясется над этим забором! Его знаешь как надо белить!
Марк Твен. Приключения Тома Сойера.

Всем, конечно, знакома удивительная штучка - лента Мебиуса. Для ее создания надо взять полоску бумаги и склеить концы, предварительно повернув один из них на пол-оборота. Вот и все хлопоты, зато теперь в наших руках самая загадочная поверхность, посланница из четырехмерного пространства. Самое удивительное ее свойство - то, что она односторонняя, ее нельзя раскрасить двумя красками, а муха, ползающая по ней, обойдет обе стороны, не пересекая край. Это свойство нашло практическое применение: запатентовано множество устройств, например, абразивный ремень для заточки, красящая лента для печатающих устройств, ременная передача и другие технические решения. Пример изобретения на основе ленты Мебиуса найдете на http://www.vlink.ru/~v-design/mebius.htm.

Кроме того, лента Мебиуса - любимый объект фантастических рассказов. В одном из них, например, пропал поезд Нью-йоркского метро, оказалось, что один из маршрутов лежал по ленте Мебиуса и поезд затерялся во времени, этот замечательный рассказ, напечатанный в журнале «Наука и жизнь» лет 30 назад, я нашел на http://www.kuzbass.ru/moshkow/koi/RAZNOE/subway.txt

Название свое лента получила в честь выдающегося немецкого математика, профессора Лейпцигского университета Августа Фердинанда Мебиуса (1790-1868), сохранявшего творческую работоспособность до конца своих дней. В работе, посвященной теории многогранников, вышедшей в 1865 году, семидесятипятилетний Мебиус впервые описал свойства односторонней поверхности.

Из множества необычных свойств этой модели расскажем лишь о самом интересном. Рассмотрим двойной лист Мебиуса, который получается, если наложить друг на друга две полоски бумаги, перекрутить их, повернув как единое целое на пол-оборота, и соединить концы. На первый взгляд кажется, что мы получаем два вложенных друг в друга листа Мебиуса. В самом деле, просунув палец между полосками бумаги и обводя им вокруг них до тех пор, пока не возвратитесь, вы «докажете», что фигура состоит из двух отдельных лент. Насекомое, заползшее в щель между бумажными лентами, могло бы совершать такое «кругосветное путешествие» до бесконечности. При этом оно всегда ползало бы по одной полоске бумаги, спинка его касалось бы другой полоски, и ему нигде не удалось бы найти точку, в которой «пол» сходится с «потолком». Отсюда наделенное разумом насекомое заключило бы, что оно путешествует между поверхностями двух отдельных полосок.

Но представим себе, что наше насекомое оставило на полу метку и совершает обход вокруг полосок до тех пор, пока не встретит ее снова. Тогда оно обнаружит, что метка находится не на полу, а на потолке и что необходимо обойти еще раз вокруг полосок, чтобы метка снова очутилась на полу! Мало того, если насекомое настроит вдоль улицы домов и будет нумеровать их слева четные, справа нечетные, то, продолжая движение, вскоре увидит слева четные, справа нечетные. Что произошло - изменились понятия левое-правое или (страшно подумать) четное-нечетное? Самое же ужасное то, что наши любимые гаишники не смогут установить правостороннее движение, ведь если вышеозначенные гипотетические насекомые будут ползти по правой стороне, то они скоро лоб в лоб столкнутся с собратьями, тоже ползущими по правой стороне улицы, правда, кто-то из них будет верх ногами, но с этим никто из них не согласится. Насекомые вряд ли должно обладать недюжинным воображением, чтобы сообразить, что и пол и потолок образуют одну сторону одной единственной полоски. То, что казалось двумя вложенными друг в друга лентами, на самом деле представляет одну большую ленту. И вы можете развернуть модель, превратив ее в одну ленту, и подумать над каверзной задачей: как придать ей снова «двухслойный» вид?
Еще множество удивительных «штучек» можно встретить в книге Мартина Гарднера «Математические головоломки и развлечения» в главе «Занимательные топологические модели». Мы же предлагаем попутешествовать (мысленно, но может кто-то отправится живьем, пусть пришлет свою фотографию).

Представьте плоское разумное существо, живущее в плоскости и не подозревающее о существовании третьего измерения. Предположим, что один из друзей отправился в путешествие, не подозревая, что по каким-то причинам плоскость, в которой они живут, оказалась лентой Мебиуса. Сделав оборот по ней и вернувшись, он предстанет перед друзьями в отраженном виде: сердце справа, ложка в левой руке, хотя он для себя не изменится, для него изменились его друзья. И тут мы, трехмерные, могли бы помочь в решении его проблемы: осторожно пинцетиком вытащить его из плоскости, перевернуть и вернуть обратно. Он снова станет нормальным, но ни за что не объяснит, что с ним произошло.

Теперь один из трехмерных наших друзей отправляется в путешествие. Физики-теоретики считают, что наша вселенная замкнута из-за гравитационного искривления пространства, а по некоторым данным, она еще и перекручена при замыкании как лента Мебиуса.

Тогда наш друг вернется со стороны, противоположной той, куда он полетел, и тоже… вы уже в курсе - отраженным. Сердце справа и левша - еще не беда, спираль ДНК в его белке закручена в другую сторону - только пол беды, но если изменилось направление вращения электронов вокруг ядер или вокруг своей оси (спин), то может произойти аннигиляция и некому будет его встречать, от Солнечной системы останется только вспышка. Поэтому кто-то из четвертого измерения должен помочь - да, да, осторожно пинцетиком вытащить его в четвертое измерение, перевернуть и осторожненько вернуть к нам. И пусть потом агент Малдер из ФБР в течение пяти серий выясняет, что произошло с нашим другом, но об этом будем знать только мы.

Также, пинцетиком, существо из четырехмерного мира может поменять правую перчатку на левую, закрученную по часовой стрелке ракушку на закрученную против часовой стрелки, может вытащить нас из замкнутой комнаты, или, наоборот, поместить в нее. Мало того, как мы, трехмерные, можем искривить плоскую ленту и переместить пинцетиком плоское существо из одной точки плоскости в другую, далекую для плоского существа, но близкую для нас трехмерных, также и нас, трехмерных, четырехмерное существо может запросто перенести как угодно далеко, в Африку, в Сызрань, на Альфу Центавра, причем без энергетических затрат - нужно только хорошо попросить, пишите.

Если вам лень путешествовать или вашим друзьям не по душе приколы с отражением и аннигиляцией, можно заняться более безобидными развлечениями. Склейте ленту Мебиуса из бумаги и разрежьте ее вдоль оси на две половинки. Предсказать результат умозрительно сможет только гений. Если вы это он, то разрежьте ленту по линии, проходящей на одну треть ее ширины от края. Предсказать заранее полученный результат не сможет даже гений. Если вам лень склеивать бумажную полоску, наберите приведенную программу в Visual Basic'e.

Private Sub Команда1_Click() R = 200 RR = 60 N = -0.5 KOL = 155 PI = 3.14159 For Fi = 0 To 365 Step ss / 2 For A = -KOL To KOL Step ss / 2 Hi = Fi * PI / 180 R1 = R + RR * Sin(Hi * N) * A / KOL W = R1 * Cos(Hi) Q = R1 * Sin(Hi) Z = RR * Cos(Hi * N) * A / KOL X = (500 + 1 * (W - Q * Cos(PI / 3))) Y = (300 + 1 * (Q * Sin(PI / 3) + Z)) Col = Форма1.BackColor If Abs(A) > 30 Then Col = RGB(Int(Abs(255 * Sin((A) / 23))), _ Int(Abs(255 * Cos(Abs(A / 25)))), Int(Abs(255 * Sin(Abs(A / 27))))) If ss > 1 Then Line (X, Y)-Step(ss, ss), Col, BF If ss = 1 Then PSet (X, Y), Col Next A Next Fi End Sub

Программа рисует на экране ленту Мебиуса. Лента получается за счет движения в пространстве отрезка вращающегося прямой. Движение замыкается в тот момент, когда отрезок совершит необходимые пол оборота. Каждый отрезок рисуется в цикле из более мелких отрезков для возможности продольной (в зависимости от A) полосатой раскраски ленты, при желании можно задать поперечную (в зависимости от Fi) или наклонные полосатые раскраски.

Продольная раскраска нужна для эксперимента: задав значение A например, более 30 при выборе цвета, увидим пустую полоску, проходящую по середине ленты и разрезающую ее на две части, что предлагалось сделать на бумажной модели. И увидим, что лента осталась неразрезанной, но стала вдвое длиннее. Программа позволит также поиграть с лентой, закручивая ее перед склеиванием на целый оборот или даже полтора и в любом направлении, делать ее шире, доводя до самопересечения, покрыть ленту пупырышками, холмами, волосками.

Вопросы - задание на дом для тех, кто что-то понял.
Можно ли забор вокруг участка земли (например, тот, который красил Том Сойер в эпиграфе) сделать в виде ленты Мебиуса?
Можно ли связать на спицах ленту Мебиуса целиком, без сшивания?
(Сложное) Какую минимальную длину должна иметь лента единичной ширины, чтобы из нее можно было бы склеить ленту Мебиуса? Подробнее о заготовке для ленты Мебиус и сопутствующих чудесах можно было прочитать в статье в «Кванте» №1 1978, доступной ныне на http://ega-math.narod.ru/Quant/Fouchs2.htm
Оцените целесообразность использования ленты Мебиуса в следующих вариантах применения: поля на рассмотренной выше шляпе, полотенце, эскалатор, туалетная бумага, шпаргалки, перфолента для станков с ЧПУ, подтяжки, шарфик, скатерть.
Представьте замкнутый брусок квадратного сечения, например, пасик от магнитофона. Мы хотим покрасить каждую грань в свой цвет. Сколько нам надо красок, если мы перед замыканием перекрутим пасик на а) 90⁰, б) 180⁰, в)270⁰, г) 360⁰?
Вы держите в руках ленту Мебиуса и смотрите на ее отражение в зеркале. Совпадают ли оно с оригиналом, есть ли ось симметрии, можно ли деформацией перевести одну ленту в другую? То есть, одинаковы ли ленты, полученные поворотом перед склеиванием в разные стороны? Долго в зеркало не смотрите, по мнению психологов это может вызвать деформацию психики, кто будет тогда заниматься лентой Мебиуса? На этой невеселой ноте и прервемся на время, чтобы набраться сил для следующего тура.

Поиск Шорька с той стороны пространства.

-Эй, Пух! - закричал Пятачок. - Здорово, Пух! Ты что там делаешь?
- Охочусь! - сказал Пух.
- Охотишься? На кого?
- Выслеживаю кого-то! - таинственно ответил Пух.
А. Милн. Винии Пух и все-все-все

Давным-давно, ещё на СМ-4, была программа (скромно уточню - моя) «Поиск Шорька». Кто такие Шорьки можно, конечно, не знать, хотя это откладывает отпечаток на стиль мышления. Это милое существо из «Алисы в Зазеркалье», гибрид штопора и хорька, к теме настоящей статьи никакого отношения вроде не имеет.
Так вот, на экран выводится поле (вроде «Сапёра» из Windows 3/95/98 или как «Lines») , а там, где стоим «мы», выводится число, показывающее наше расстояние до Шорька. Перемещаясь по полю и анализируя меняющееся расстояние до Шорька, пытаемся его настигнуть. Хитрющий Шорёк тоже передвигается, усложняя нашу задачу. Зону игры можно замкнуть по вертикали и по горизонтали, образовав тор и гоняться за Шорьком по тору. Уходя за правую границу поля, мы появляемся слева, уходя вниз, появимся сверху.
Причем, можно замкнуть пространство только для «нас», а Шорька ограничить границами поля - тогда он быстро ловится. А если наоборот - для Шорька замкнуть, а для «нас» нет, то достать его будет довольно трудно. Но все в наших руках, точнее головах, еще точнее - додумайте сами, я запутался. Итак, текст программы на Borland Pascal'e 7.0 для DOS'a.

PROGRAM Shorjok; USES CRT,GRAPH,DOS; VAR R,M,S,X,Y,XX,YY,X0,Y0,I,J : INTEGER; QQ,CH,CH1: STRING; GraphDriver,GraphMode:INTEGER ; {+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++} BEGIN RANDOMIZE ; X0:=RANDOM(11) ; Y0:=RANDOM(11) ; {1} GraphDriver:= Detect; InitGraph(GraphDriver,GraphMode,''); SETLINESTYLE(0,0,1); XX:=4 ; YY:=5 ; {2} SETFILLSTYLE(1,0) ; BAR(0,0,640,480) ; SETFILLSTYLE(1,7) ; REPEAT Y:=40 ; M:=40 ; S:=3 ; REPEAT X:=120 ; REPEAT BAR(X,Y,X+M,Y+M) ; X:=X+M+S; UNTIL X > 520 ; Y:=Y+M+S ; UNTIL Y>400+M ; setcolor(15); settextstyle(0,0,3) ; R:=ROUND(SQRT((XX-X0)*(XX-X0)+(YY-Y0)*(YY-Y0))) ; STR(R,QQ) ; {3} outtextxy(120+(XX-1)*M+XX*S-3,40+(YY-1)*M+YY*S,QQ); ch1:=readkey; if ch1=#27 then EXIT; if ch1=#0 then ch:=readkey; {4} if ch='K' then XX:=XX-1; {5) if XX<1 then XX:=XX+10 ; if ch='M' then XX:=XX+1; if XX>10 then XX:=XX-10 ; if ch='H' then YY:=YY-1; if YY<1 then YY:=YY+10 ; if ch='P' then YY:=YY+1; if YY>10 then YY:=YY-10 ; X0:=X0+RANDOM(3)-1 ; if X0<1 then X0:=X0+10 ; if X0>10 then X0:=X0-10 ; Y0:=Y0+RANDOM(3)-1 ; if Y0<1 then Y0:=Y0+10 ; if Y0>10 then Y0:=Y0-10 ; {6} UNTIL CH=#27 ; CLOSEGRAPH; END.

В двух словах о программе. Переменные X0 и Y0 - координаты Шорька, выбираются и изменяются случайным образом, XX и YY - наши координаты, в которых выводится расстояние до Шорька. В строке 4 опрашивается клавиатура, причем обрабатываются только клавиши со стрелками и для выхода. После каждого нашего шага поле перерисовывается, убирая предыдущее расстояние с экрана.
Просьба не критиковать слишком скромный интерфейс программы, можно, конечно, сделать поле объемным, дать тени, название, подсказки, задействовать мышку и прочие накрутки (как в CDMan, Packman и прочих удирающих от монстров колобках) - это все после, и так вступление (а это все было вступление) затянулось и не терпится перейти к тому, что поинтересней. (Самой приятной «фичей» было бы сделать нашу скорость больше, чем у убегающего Шорька, но придать нам инерцию…)
Итак, встряхните опилки в голове и сосредоточьтесь. Это всё было подготовкой к следующему шагу - при замыкании зоны по горизонтали (мысленно конечно же), перекрутим её на 180⁰, как ленту Мёбиуса. Полученное тело называется бутылкой Клейна (в честь немецкого математика Феликса Клейна, подробнее о нем смотрите на http://users.omskreg.ru/~project/VM/klein.html) и не может существовать в трёхмерном мире, но ничто не помешает нам гоняться по нему за Шорьком. Достаточно исправить соответствующие команды «замыкания» поверхности между {5} и {6}.
Уйдя вправо сверху мы появимся слева внизу, но это будем уже не совсем мы, а как бы мы с другой ориентацией, отражённые мы. Сможем ли такие мы поймать Шорька, если он остался «с этой стороны»? Тут надо крепко подумать. Учитывая, что все в наших руках (см. выше), можно разрешить нам, потусторонним, не боясь аннигиляции, зацапать «тутошнего» Шорька. Или наоборот, запретить «отраженцам» являться в реальный мир и выводить расстояние с учетом перехода через переворачивающий край.
Можно, например, менять цвет выводимых цифр, если мы с Шорьком по разные стороны поверхности.

Бутылка Клейна необычайно интересная модель. Если вы замкнете квадратное поле по горизонтали, получив цилиндр, и попытаетесь замкнуть по вертикали - то получим обычный тор. (О торе мы уже писали в журнале Hard'n'Soft #9 2001), смотрите статьи Рогатая гусеница и Бублики, планеты и колечки дыма.
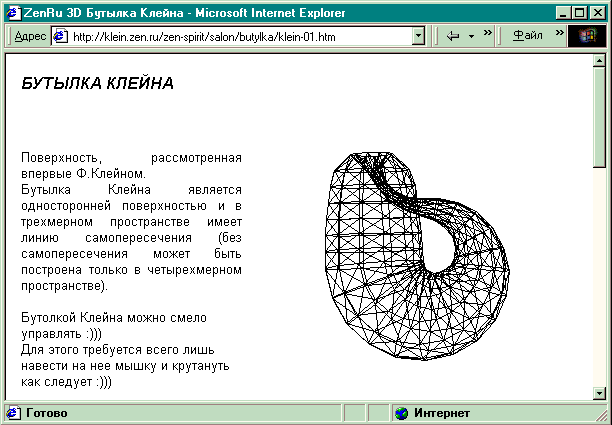
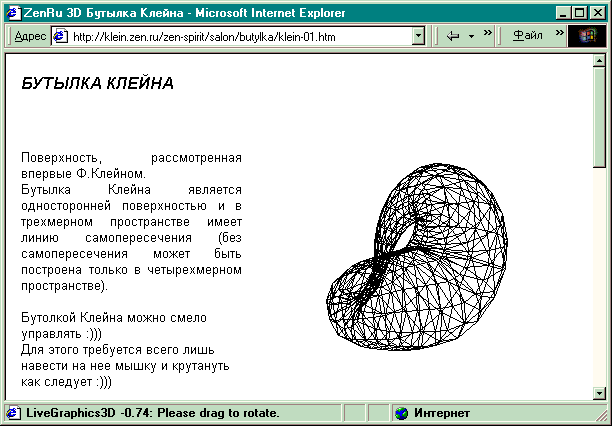
Необходимо перед замыканием по вертикали поменять ориентацию поверхностей, для этого надо замыкать цилиндр не снаружи, как тор, а изнутри, проткнув поверхность цилиндра. В трехмерном пространстве нельзя построить бутылку Клейна без самопересечения, это как бы ее модель, на самом то деле она без пересечений, утоньшений и перегибов. Представить ее довольно трудно, тут здорово поможет аплет, расположенный на http://klein.zen.ru/zen-spirit/salon/butylka/klein-01.htm. С его помощью можно хорошенько рассмотреть бутылку, поворачивая ее мышкой, спасибо разработчикам!

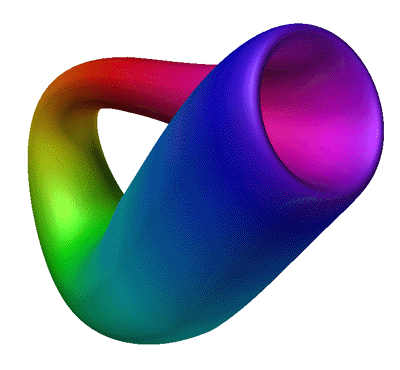
А если перед замыканием по вертикали тоже перекрутить на 180⁰, то получим проективную плоскость, которую вообще невозможно представить нормальному человеку. Теперь понадобятся не только опилки, но и иголки с булавками (как у Страшилы из Изумрудного Города). Подумайте, если мы два раза «перевернёмся»: по вертикали и по горизонтали, то сохраним ли ориентацию (в смысле часы на левой руке, а ложка в правой), и где окажемся - внутри или снаружи? Над или под? О Шорьке забыли (уже не до Шорька?). Можем ли мы, перевернувшись по вертикали, неожиданно столкнуться с Шорьком, перевернувшимся по горизонтали, или мы друг друга не увидим? Устали путешествовать? Вернитесь в исходное состояние в смысле часов и ложки. Возвращаться надо очень осторожно, ибо, даже проверив, что сердце булькает слева, а пломба в зубе и любимый пробор справа, еще не значит, что вы правильно вернулись, так как для путешествующего свои лево- право не меняются, а меняется окружающий мир. Например, может оказаться, что после возвращения ваши личные часы идут назад - вы сначала падаете, потом спотыкаетесь и при этом молодеете. Или спираль вашей ДНК закручена в другую сторону чем у сыра, которым вы, утомившись там, хотите подкрепиться здесь. Приведенная программа с минимальными доработками позволит испытать (без сыра, разумеется) различные эффекты от совместной прогулки с Шорьком. Можно было бы еще придать Шорьку инерцию, задать тяготение или ветер, сделать два-три Шорька, мины, жизни, уровни, ловушки - но это все уже где то было, сегодня наша единственная цель - путешествовать по поверхностям наблюдая за своими ощущениями. Поэтому истинным ценителям и храбрецам-Сталкерам можно рекомендовать прогуляться вблизи Черной дыры - я побоялся, немногие вернувшиеся говорят, что там пространство и время меняются местами. А публике попроще предлагаем побродить по поверхности в виде чашки с двумя ручками (одна внутри), потом расскажите, кого там встретили.

Ссылки:

1. http://www.math.ohio-state.edu/~fiedorow/math655/Klein2.html Страничка университета Огайо рассказывает о бутылке Клейна с иллюстрацией ее свойств интересным аплетом, выложен и код для любителей экспериментов. (на английском языке)

2. http://klein.zen.ru/zen-spirit/salon/butylka/klein-02.htm здесь вы найдете занимательный и слегка сомнительный материал на тему "Реторта" Клейна - модель черной дыры??? ". (на английском языке)

3. http://www.math.ucla.edu/~jimc/klein_h/index.shtml о гравитационных парадоксах в бутылке Клейна (на английском языке)

4. http://www.math.rochester.edu/misc/klein-bottle.html о бутылке Клейна (на английском языке) с хорошей картинкой.

5. http://comp.uark.edu/~cgstraus/k/klein.html руководство по изготовлению бутылки Клейна. (на английском языке)

6. http://www.oldsf.com/ZF/0_prof.html Наука и жизнь, 1977, № 5. М. ГАРДНЕР. ПРОФЕССОР, У КОТОРОГО НЕ БЫЛО НИ ОДНОЙ СТОРОНЫ

7. http://golovolomka.hobby.ru/books/gardner/fivemap.shtml Мартин Гарднер: Остров пяти красок

8. http://pantheon.yale.edu/~jar55/math/project/index.html обзор поверхностей и их свойств (на английском языке) с красивой картинкой.