
|
|
|
|
|
|
|
|
|
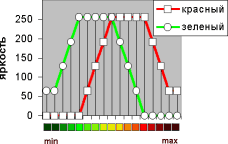
Нелинейные поверхности и цветовые гаммыВизуализация графиков функций двух переменных вида z=f(x,y) - часто возникающая практическая задача. Кроме того, эти нелинейные поверхности бывают невероятно интересных, красивых форм. Их исследование само по себе - крайне занимательный и поучительный процесс. Строить графики функций двух переменных на компьютере можно различными способами. В одном из прошлых номеров "КВ" уже обсуждался этот вопрос. Тогда речь шла о тоновой визуализации с использованием различных градаций серого цвета. Монохромные изображения обладают своим неповторимым шармом, некоей внутренней загадочностью. Недаром многим людям черно-белые снимки нравятся больше, чем цветные, а черно-белая фотография сохраняет свои позиции в высоком фотоискусстве несмотря ни на какие изыски научно-технического прогресса. Тем не менее, цвет - мощнейшее изобразительное средство. Если при визуализации графика функции z=f(x,y) воспользоваться не черно-белой, а цветной палитрой, то информативность такого изображения резко возрастет. Для воспроизведения округлых и пластичных форм нелинейных поверхностей лучше всего подходят палитры, содержащие плавные взаимопереходы различных цветовых оттенков. Использование градаций серого тона позволяет моделировать игру света и тени. Замена же монохромной шкалы тонов непрерывной цветовой гаммой, например, от темно-зеленого через ярко-желтый к ярко-красному и далее до темно-красного, позволяет резко усилить выразительность и наглядность графика. Как известно, любой цвет формируется на экране монитора всего из трех "чистых" цветовых компонент - красного (Red), зеленого (Green) и синего (Blue). Каждый пиксел, если рассматривать экран через увеличительное стекло, состоит из трех зернышек красного, зеленого и голубого цвета. Эти зернышки могут светиться с различной интенсивностью. В зависимости от яркости свечения основных цветовых компонент, отдельные точки сливаются издалека в различные однородные цвета. Современное электронное оборудование (в режиме TrueColor) позволяет варьировать яркость свечения каждой из цветовых компонент на 256 уровнях (от 0 до 255 единиц). Таким образом, максимальное количество возможных цветовых комбинаций равно 256*256*256, что примерно составляет 16,7 миллионов цветовых оттенков. В нашем случае для раскраски графика функции двух переменных z=f(x,y) используем палитру, содержащую различные смеси зеленого (G) и красного (R) тонов. Глубокие впадины на поверхности z будем закрашивать темно-зеленым цветом, который по мере увеличения z будет постепенно становиться все ярче, переходя в ярко-зеленый, а затем в желтый. При дальнейшем увеличении z заставим поверхность постепенно краснеть. И, наконец, самые высокие "холмы" на графике будем обозначать темным кроваво-красным тоном. Описанное цветовое решение изображено на графике.
Его суть состоит в следующем. Исследуемый интервал значений z от минимума до максимума разбивается на четыре равные части. Все точки изображаемой поверхности, в которых значение z меньше заданного zmin, окрашиваются в темно-зеленый цвет (G=63). Далее, в первой четверти интервала, зеленая компонента постепенно возрастает от 63 до 255. При этом все остальные цвета сохраняют свои нулевые значения. Во второй четверти зеленая компонента сохраняет максимальное значение, и постепенно от 0 до 255 возрастает яркость красного цвета. Таким образом, во второй четверти ярко-зеленый цвет постепенно переходит в ярко-желтый. В третьей четверти яркость зеленого цвета падает от 255 до 0, но красный сохраняет свою максимальную интенсивность. В третьей четверти ярко-желтый постепенно переходит в чистый ярко-красный цвет. И, наконец, в последней четвертой четверти ярко-красный плавно "затухает" до мрачного темно-кровавого оттенка (R=63). И далее все точки поверхности, в которых z принимает значения больше заданного zmax, окрашиваются в темно-красный цвет. Визуально оценить описанную палитру можно, заменив стандартный набор цветов простейшего графического редактора Paint цветовыми комбинациями, приведенными в таблице (значения в таблице соответствуют точкам на графике).
Те же самые "фокусы" можно проделывать и с другими цветовыми переходами, например, от темно-синего к небесно-голубому и далее к зеленому и т.д. Порядок смешивания цветов можно менять произвольным образом. Важен сам принцип постепенности. Сначала нарастает (убывает) одна компонента, затем к ней постепенно присоединяется другая. Потом они могут меняться местами и т.д. Все определяется вашим художественным вкусом и интуицией. Для построения цветных графиков функций двух переменных легко может быть адаптирована обсуждавшаяся ранее программная процедура тоновой визуализации (см. "КВ" №29). Вот ее модифицированный вариант: DefSng X-Z Dim Zmin As Single Dim Zmax As Single Dim R As Single Dim R4 As Single Dim Z14 As Single Dim Z24 As Single Dim Z34 As Single Private Sub Screen_Click() Dim c As Long Dim n As Integer Dim hx As Single Dim hy As Single n = 405 Xmin = Text1(0).Text Xmax = Text1(1).Text Ymin = Text1(2).Text Ymax = Text1(3).Text Zmin = Text1(4).Text Zmax = Text1(5).Text R = Zmax - Zmin R4 = R / 4 Z14 = Zmin + R4 Z24 = Z14 + R4 Z34 = Z24 + R4 hx = (Xmax - Xmin) / n hy = (Ymax - Ymin) / n y = Ymin - hy / 2 For j = 0 To n x = Xmin - hx / 2 y = y + hy For i = 0 To n x = x + hx z = f(x, y) c = SetColor(z) Screen.PSet (i, j), c Next i Next j End Sub Public Function f(x As Single, y As Single) As Single f = Sin((y ^ 3 - x ^ 2) * (x - x * y)) End Function Public Function SetColor(z As Single) As Long Dim t As Byte Select Case z Case Is <Zmin SetColor="RGB(0," 63, 0) Case Zmin To Z14 t="63" + 192 * (z Zmin) / R4 SetColor="RGB(0," t, 0) Case Z14 To Z24 t="255" * (z Z14) / R4 SetColor="RGB(t," 255, 0) Case Z24 To Z34 t="255" * (1 (z Z24) / R4) SetColor="RGB(255," t, 0) Case Z34 To Zmax t="63" + 192 * (1 (z Z34) / R4) SetColor="RGB(t," 0, 0) Case Is> Zmax SetColor = RGB(63, 0, 0) End Select End Function В начале программы добавлен расчет величины и
границ подинтервалов, необходимых для
дальнейших вычислений. Андрей КОЛЕСНИКОВ,
Построение трехмерных графиков функций двух переменныхГрафики функций двух переменных вида z=f(x,y), в отличие от графиков функций y=f(x), представляют собой не линии, а поверхности. Если график функции y=f(x) можно легко изобразить на плоском листе бумаги, то график функции z=f(x,y) уже не помещается на плоскости, а требует пространственного представления. В прошлых номерах "КВ" (см. "КВ" №29, 1999 г. и №2, 2000 г.) рассматривались способы построения графиков функций двух переменных, основанные на тоновой и цветовой визуализации. Суть этих методов состоит в том, что значениям z ставится в соответствие некая шкала тонов или цветовая гамма. Иными словами, сама картинка строится на плоскости в координатах x и y, а третье пространственное измерение моделируется при помощи игры полутонов или цветовых оттенков. Весьма интересно, однако, было бы увидеть не только плоское изображение графика, но и его пространственную реконструкцию. В изобразительном искусстве и черчении различные объекты моделируются на плоскости рисунка или чертежа в виде тех или иных трехмерных проекций. Рассмотрим один из возможных методов адаптации программы тоновой визуализации для построения трехмерных проекций графиков функций двух переменных. Наиболее удобна для компьютерной реализации так называемая фронтальная диметрическая проекция. В ней ось X располагается горизонтально, ось Z - вертикально, а ось Y - под углом 45° к горизонтальной оси X. При фронтальном диметрическом проецировании размеры по оси Y необходимо делать вдвое меньшими, чем аналогичные размеры по осям X и Z. За основу программы возьмем код процедуры тоновой визуализации ("КВ" №29, 1999 г.). Для того, чтобы преобразовать плоское тоновое изображение в его аксонометрическую проекцию, при построении картинки будем каждую новую строку пикселов сдвигать на одну позицию вправо. Таким образом, квадрат превратится в параллелограмм, острые углы которого будут примерно равны 45°. Картинка окажется как бы лежащей на полу. Для имитации двукратного уменьшения размеров по оси Y уменьшим наполовину количество строк пикселов по сравнению с количеством пикселов в одной строке. Величину z для каждой из точек будем интерпретировать не только как тон пиксела, но и как расстояние от "пола" до точки трехмерного графика. В соответствующей позиции над плоскостью XY будем ставить точку черного цвета. В результате работы программы над лежащей тоновой тенью повиснет легкое точечное изображение трехмерного каркаса исследуемой поверхности, чем-то напоминающее натянутый прозрачный черный нейлон (см. рисунки). В том случае, когда на одном рисунке совмещается тоновое изображение с "парящей" над ним трехмерной структурой, можно составить наиболее полное и адекватное представление о пространственной форме графика функции. От нас уже не ускользнут различные детали, заслоненные "холмами" на переднем плане. В то же самое время можно будет получить достаточно наглядное и полное впечатление о рельефе поверхности. Ниже приведен программный код процедуры, реализующей описанный алгоритм. DefSng X-Z Public Function f(x As Single, y As Single) As Single f = Sin(x * y / 2) End Function Private Sub Screen_Click() Dim c As Long Dim t As Byte Dim n As Integer Dim hx As Single Dim hy As Single Dim Rz As Single Screen.Cls n = 300 m = 150 xmin = Text1(0).Text xmax = Text1(1).Text ymin = Text1(2).Text ymax = Text1(3).Text zmin = Text1(4).Text zmax = Text1(5).Text Rz = zmax — zmin hx = (xmax — xmin) / n hy = (ymax — ymin) / m y = ymin — hy / 2 For j = 300 To 450 x = xmax + hx / 2 y = y + hy For i = j To (j — 300) Step -1 x = x — hx z = f(x, y) Select Case z Case Is > zmax c = RGB(200, 200, 200) k = n Case Is < zmin c = RGB(0, 0, 0) k = 0 Case zmin To zmax t = 255 * (z — zmin) / Rz k = 300 * (z — zmin) / Rz c = RGB(t, t, t) End Select Screen.PSet (i, j), c Screen.PSet (i, j — k), RGB(0, 0, 0) Next i Next j End Sub При помощи приведенной программы можно получить бесчисленное множество пространственных изображений различных функций. Мы уже имели возможность оценить богатство их форм и красоту, проводя опыты с тоновой визуализацией. Объемные графики весьма существенно дополняют тоновые изображения. Они в полной мере позволяют оценить неповторимую пластику нелинейных поверхностей, среди которых порой попадаются весьма изысканные и привлекательные формы, доставляющие истинное эстетическое наслаждение. Компьютерная визуализация многократно усиливает творческий потенциал геометрического мышления, стимулирует пространственное воображение, что, несомненно, способствует дальнейшему познанию загадочного и необычайно красивого мира чисел. Визуализация графиков функций двух переменных имеет не только эстетическое, но и практическое значение. Функции двух переменных нередко выступают в качестве математических моделей различных процессов. После того, как эта модель становится зримой, анализировать ее гораздо проще. Закономерности течения исследуемого явления становятся видимыми и очевидными. На графиках отчетливо прослеживается местоположение экстремальных точек. А поиск минимумов или максимумов функции, описывающей какой-то физический или производственный процесс, имеет прямое отношение к решению различного рода оптимизационных задач. Судя по письмам, при повторении программ, приводимых в моих статьях, у читателей нередко возникает одна и та же ситуация, когда вместо полной картинки в графическом окне появляется лишь ее микроскопическая копия. Это вовсе не какой-то коварный глюк, а всего лишь следствие того, что я привык измерять экранное пространство в пикселах, а не в твипах. В VB же по умолчанию в качестве экранных единиц измерения предлагаются именно твипы. Твипы гораздо мельче пикселов (1 логический сантиметр - 567 твипов), поэтому итоговая картинка получается микроскопической. Для того, чтобы этого избежать, необходимо поменять единицы измерения с твипов на пикселы (свойство ScaleMode). Андрей КОЛЕСНИКОВ,
Просто пузыриПо древней легенде, прекрасная Афродита родилась из морской пены. Как и во многих древних мифах, в этой красивой сказке скрыт глубокий космогонический смысл. В пене действительно есть что-то тайное, метафизическое. Попробуйте пристально вглядеться в структуру пены (для этого, например, можно использовать бокал пива или поролоновую губку). В этих эфемерных трехмерных кружевах интуитивно угадываются некие базовые проэлементы будущих клеточных тканей живых организмов. Именно пена, которая образовывалась на поверхности первичного океана Земли миллиарды лет назад, послужила той изначальной субстанцией, из которой впоследствии возникла жизнь. Этот процесс физико-химической самоорганизации продолжался многие миллионы лет и занял гораздо больше времени, чем вся последующая биологическая эволюция. Древняя пена постепенно усложнялась, обогащалась сложными химическими веществами, обретала способность к самовоспроизведению, дыханию и, наконец, ожила. Представить себе величественный космический процесс становления жизни можно, обратившись к удивительной живописной серии известного литовского композитора и художника Чурлёниса. По признанию самого автора, он собирался работать над этой серией всю свою жизнь. Рисунки объединены под общим названием "Сотворение мира" и отображают различные стадии эволюции от первичного сгустка космической плазмы до образования ростков жизни в древнем, возможно, неземном, планетарном океане (ознакомиться с серией "Сотворение мира" можно по адресу neris.mii.lt/art/ciurlionis/creation/cretion.html). Такой поток ассоциаций нахлынул на меня после посещения очень интересного сетевого ресурса под названием "Арбуз или угощение для технической интеллигенции" (http://www.arbuz.narod.ru/). Читателям, интересующимся различными занимательными математическими феноменами и программированием, я настоятельно рекомендую посетить этот адрес - не пожалеете. В числе прочего на сайте выложена и страничка о пузырях и пене. Идея алгоритма проста. Вначале случайным образом разыгрывается некоторое заданное количество точек на участке плоскости. Это центры будущих пузырей. Далее последовательно для каждой точки строящегося изображения вычисляются расстояния от нее до всех центров. Из них выбирается наименьшее, и, в зависимости от его значения, точка окрашивается в соответствующий тон. В результате получается некое подобие пены. В программе, выложенной на сайте, включен дополнительный цикл для пузырьковой сортировки (в данном случае термин "пузырьковая сортировка", как вы понимаете, никак не связан с обсуждаемой темой) расстояний. Это, по-моему, будет здорово замедлять работу программы с ростом количества пузырей. Поэтому я переписал программный код следующим образом: Dim i As Byte Dim n As Byte Dim x_bubble(100) As Integer Dim y_bubble(100) As Integer Dim x As Integer Dim y As Integer Dim r(100) As Single Dim r_min As Single Dim PointColor As Long Private Sub Form_Click()
Cls
Randomize
n = 25
For i = 1 To n
x_bubble(i) = Rnd * 500
y_bubble(i) = Rnd * 500
Next i
For x = 1 To 500
For y = 1 To 500
r_min = 2000
For i = 1 To n
r(i) = Sqr((x_bubble(i) - x) ^ 2 + (y_bubble(i) - y) ^ 2)
If r_min > r(i) Then r_min = r(i)
Next i
PointColor = RGB(255 - Int(r_min), 255 - Int(r_min), 255 - Int(r_min))
PSet (x, y), PointColor
Next y
Next x
End Sub
Варьируя коэффициенты при различных цветовых компонентах в функции RGB, можно получать пену различных цветовых оттенков. Если же изменять количество исходных центров пузырей, то итоговая пена будет получаться различной степени насыщенности. С помощью приведенного программного фрагмента я получил несколько загадочных изображений, напоминающих не то молекулы, не то кладки икры инопланетной твари. Одно из них я даже сделал покрытием для рабочего стола. Как это ни парадоксально, но у многих людей эти картинки вызывают некие устойчивые эротические ассоциации. Не правда ли, напоминает известный анекдот о том, как пациент спрашивает у доктора, демонстрирующего ему психологические тесты в виде квадратов и треугольников: "Доктор, а откуда у вас такие неприличные картинки?".
А. КОЛЕСНИКОВ,
Тоновая визуализация нелинейных поверхностейЖивопись света - так критики характеризуют творчество современной немецкой художницы Рут Хюблер. Она работает в уникальной, присущей только ей манере ступенчатой техники живописи. Картины Рут Хюблер строятся, как правило, на основе какой-то геометрической фигуры, разделенной на отдельные сегменты. Все сегменты исходной геометрической конструкции раскрашиваются в тона одного и того же цвета различной интенсивности. Цвет располагается так, что интенсивность тона плавно изменяется от одного соседнего сегмента к другому. Таким образом, создается впечатление, что все изображение как бы состоит из света, преломленного тем или иным причудливым образом. Например, если светлый тон концентрируется в центре композиции и плавно затухает по ее краям, то зритель воспринимает сюжет такой картины как размытое изображение некого светящегося объекта. Идея светописи Рут Хюблер может оказаться полезной не только в изобразительном искусстве, но и в области компьютерной визуализации. Компьютерная визуализация имеет исключительное значение для современной насквозь математизированной науки. Абстрактные математические формулы недостаточны для полноценного познания сути того или иного объекта или явления. Всегда хочется знать, как э т о "выглядит". Человеку в силу его ментальной организации необходимы наглядные образы. И здесь компьютерная визуализация совершенно необходима. Рассмотрим задачу визуализации нелинейной поверхности, описываемой функцией вида z=f(x, y). Задачи подобного рода часто возникают при анализе математических моделей изменения некоторого параметра z в зависимости от пространственных координат x и y. Речь может идти о картине распределения теплых и холодных воздушных масс на карте города, о зонах с различными физическими характеристиками на поверхности какого-то испытуемого образца нового сплава и о многих других подобных задачах. Решить проблему можно, построив трехмерный "проволочный каркас" исследуемой поверхности. Это будет, однако, не самое простое, а в некоторых случаях и не самое удобное решение. В трехмерной проекции отдельные крупные "холмы" на переднем плане могут заслонить другие, не менее важные детали на заднем плане. Кроме того, в трехмерном варианте возможны определенные проблемы с визуальной оценкой координат тех либо иных деталей рельефа исследуемой поверхности. Одним из наиболее простых и удобных способов посмотреть, что же внешне представляет собой график интересующей нас функции z=f(x, y), состоит в представлении поверхности z как мозаичного панно, состоящего из отдельных тонированных квадратиков (пикселов). В этом случае мы как бы смотрим сверху на залитую светом поверхность перпендикулярно плоскости (x,y). Необязательно составлять мозаику именно из отдельных пикселов и вычислять значение функции для каждого из них, что, разумеется, резко увеличивает время расчетов. Наглядное представление о форме поверхности можно получить, даже если просто покрыть исследуемый участок координатной плоскости достаточно мелкой квадратной сеточкой и вычислить значения z для каждой ее ячейки. При этом точкой, определяющей цвет отдельного квадратика, можно выбрать его центр, а потом, в зависимости от значения функции в этой точке, окрашивать весь квадратик. Для того, чтобы игра света и тени адекватно отображала впадины и выпуклости на исследуемой нелинейной поверхности, значение z в каждом из квадратиков удобно изображать соответствующим уровнем яркости свечения пикселов. Например, чем выше значение z, тем ярче светится квадратик, и наоборот, чем меньше значение z в ячейке, тем в более темный тон она окрашивается. То есть, можно каждой точке исследуемого прямоугольного участка приписать определенное значение цвета, которое будет тем или иным образом соответствовать значению z в данной области. Например, при использовании палитры, содержащей плавный переход от черного к белому, большим значениям z можно поставить в соответствие более светлый тон свечения пикселов, а более малым значениям z поставить в соответствие более темный тон. Тогда впадины будут скрыты густой тенью, а выпуклости или возвышенности, напротив, будут ярко освещены. Ниже приводится фрагмент программного кода на Visual Basic, позволяющий строить тоновые графики функций двух переменных. DefSng X-Z Public Function f(x As Single, y As Single) As Single f = Sin((y * x - x ^ 2) * (x - x * y)) End Function Private Sub Screen_Click() Dim c As Long Dim t As Byte Dim n As Integer Dim hx As Single Dim hy As Single n = 500 xmin = Text1(0).Text xmax = Text1(1).Text ymin = Text1(2).Text ymax = Text1(3).Text zmin = Text1(4).Text zmax = Text1(5).Text hx = (xmax - xmin) / n hy = (ymax - ymin) / n y = ymin - hy / 2 For j = 0 To n x = xmin - hx / 2 y = y + hy For i = 0 To n x = x + hx z = f(x, y) Select Case z Case Is > zmax c = RGB(255, 255, 255) Case Is < zmin c = RGB(0, 0, 0) Case zmin To zmax t = 255 * (z - zmin) / (zmax - zmin) c = RGB(t, t, t) End Select Screen.PSet (i, j), c Next i Next j End Sub Необходимыми исходными данными для программы являются: вид функции z=f(x, y), задаваемый в отдельной подпрограмме-функции; минимальные и максимальные значения координат Xmin, Xmax, Ymin, Ymax, ограничивающие исследуемый участок числовой плоскости; минимальное и максимальное значение Zmin, Zmax. Заранее точно знать последние два параметра удается не всегда. Поэтому все квадратики, в которых f(x, y) принимает значения меньшие заданного Zmin, окрашиваются в черный цвет (RGB(0,0,0)), а все квадратики, в которых f(x, y) принимает значение больше заданного Zmax, окрашиваются в белый цвет (RGB(255,255,255)). Все необходимые числовые значения считываются после щелчка мыши на объекте screen (PictureBox) из отдельных текстовых окошек, объединенных в массив объектов. В приведенной процедуре поверхность строится с точностью до пиксела. Если же строить график на более крупной масштабной сеточке, то метод Pset следует заменить на метод Line с параметром BF.
А. КОЛЕСНИКОВ,
Фигуры в криволинейных координатахКроме привычной нам прямоугольной декартовой системы координат, в математике используются и другие способы задания положения точки в пространстве или на плоскости. Чаще всего применяются полярные, цилиндрические и сферические координаты. Все эти системы родственны. В них присутствует центральная точка или полюс, от которого расходятся концентрические окружности (полярная система координат), цилиндры (цилиндрическая система) или сферы (сферические координаты). Положение точки определяется при помощи луча, выходящего из полюса и пересекающего в заданном месте соответствующую окружность, цилиндр или сферу. В такие координаты очень естественно укладываются многие природные формы. Например, если вновь открыть уже упоминавшийся атлас Геккеля, то многие из изображенных там организмов легко можно поместить в одну из этих систем координат, а затем и подобрать математическое выражение, описывающее их внешние контуры. Перечисленные криволинейные системы координат идеально приспособлены для отображения форм, построенных вокруг единой центральной точки. Такая организация характерна для многих биологических объектов. Их формы порой самым удивительным образом напоминают фигуры, образуемые в криволинейных координатах достаточно простыми и лаконичными математическими выражениями. Это сходство указывает на то, что тела живых организмов, биологические структуры, образуются по принципам, сходным с принципами построения "полярных" объектов. Живой организм "начинается" из одной исходной точки, и затем развивается и растет во все стороны по определенному математическому закону. По крайней мере такое предположение совсем не противоречит наблюдаемому в природе обилию "математических", "полярных" форм. Природа как бы сама использует полярные координаты, что особенно бросается в глаза на примере растений, примитивных многоклеточных животных и насекомых. Вероятно поэтому фигуры, построенные в полярных координатах, обладают неповторимой эстетической привлекательностью. Они плотно ассоциируются с формами цветов, бабочек, словом, всем тем, что так много удовольствия доставляет нашему взору в живой природе. В полярной системе координат положение точки определяется полярным радиусом r и углом j, образуемым полярным радиусом с полярной осью. Если в декартовой системе координат предельно простое выражение y=kx определяет прямую линию, то это же выражение, переписанное в форме r=kj, уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. В цилиндрической системе к полярному радиусу и углу добавляется еще одна координата - z, которую можно интерпретировать как высоту точки над плоскостью, в которой вращается полярный радиус.
Dim r As Byte Dim g As Byte Dim b As Byte Dim i As Integer Dim j As Integer Dim Rmax As Single Dim Ro As Single Dim fi As Single Function f(fi As Single, a As Single) As Single f = 2 * (1 + Cos(fi)) End Function Sub Screen_click() screen.Cls Rmax = Text1.Text pi = 3.141593 For fi = 0 To 2 * pi Step 0.001 * pi Ro = f(fi, a) x = Ro * Cos(fi) y = Ro * Sin(fi) i = 300 * (x + Rmax) / (2 * Rmax) j = 300 - 300 * (y + Rmax) / (2 * Rmax) ... screen.PSet (i, j), RGB(r, g, b) Next fi End Sub Цвет в программу можно добавлять "по вкусу". Для вычисления значений байтовый цветовых переменных r, g и b возможны различные способы (избранный алгоритм следует вставить в программу вместо многоточия). Интересные цветовые эффекты получаются, если поставить значения цветовых компонент в зависимость от r. Для визуализации структур, заданных в цилиндрических координатах, я использовал программу, описанную в КВ №2, 13-19 января 2000 года. Необходимо лишь добавить в подпрограмму-функцию обратное преобразование декартовых координат в цилиндрические, а затем вычислить значение z по той или иной "цилиндрической" формуле. Public Function f(x As Single, y As Single) As Single ro = Sqr(x ^ 2 + y ^ 2) fi = Atn(y / x) cosfi = x / ro sinfi = y / ro f = (1 - (cosfi) ^ 2 / (ro)) ^ 2 End Function В текст основной процедуры следует добавить ввод значения Rmax. После проделанных преобразований программа будет отображать зависимость переменной z от полярного радиуса и угла.
А.КОЛЕСНИКОВ, |
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|
 Вместо
простого определения интенсивности серого тона
в текущей точке в программу добавлена функция
вычисления цвета SetColor(z). Цветное изображение,
полученное при помощи данной модифицированной
процедуры, приведено на рисунке. Поскольку
"КВ" выходит в черно-белом формате,
читателям придется поверить мне на слово, либо
воспроизвести описанные вычисления на своих
компьютерах самостоятельно. Уверен, что, не
поленившись все это проделать, вы будете
вознаграждены сторицей за свои труды
открывшимися перед вашим взором многоцветными
красотами виртуального мира математической
нелинейности. Если же кто-то из вас найдет время
поделиться результатами своих находок и
экспериментов с цветом и математикой, -
присылайте... Благодарю всех читателей,
приславших мне свои вопросы, соображения и
предложения в прошедшем году. Все они не
останутся без внимания.
Вместо
простого определения интенсивности серого тона
в текущей точке в программу добавлена функция
вычисления цвета SetColor(z). Цветное изображение,
полученное при помощи данной модифицированной
процедуры, приведено на рисунке. Поскольку
"КВ" выходит в черно-белом формате,
читателям придется поверить мне на слово, либо
воспроизвести описанные вычисления на своих
компьютерах самостоятельно. Уверен, что, не
поленившись все это проделать, вы будете
вознаграждены сторицей за свои труды
открывшимися перед вашим взором многоцветными
красотами виртуального мира математической
нелинейности. Если же кто-то из вас найдет время
поделиться результатами своих находок и
экспериментов с цветом и математикой, -
присылайте... Благодарю всех читателей,
приславших мне свои вопросы, соображения и
предложения в прошедшем году. Все они не
останутся без внимания.

 Поэкспериментировав
с различными функциями, можно убедиться в том,
что простые нелинейные выражения нередко
определяют поверхности сложнейшей изысканной
формы. Мир математической нелинейности (как,
впрочем, и мир окружающей нас физической
реальности) неимоверно богат и разнообразен. Кто
знает, какие тайны еще скрыты в его глубинах.
Исследование функций двух переменных - крайне
занимательное занятие само по себе. Слегка
изменяя вид функции и масштаб картинки, можно
получить бесконечный ряд фантастически красивых
математических "пейзажей". Кроме того, такие
компьютерные экскурсии в мир математической
нелинейности весьма поучительны. Они развивают
способность иначе видеть окружающий нас мир и
гораздо глубже понимать его законы. Анализ
отдельных графиков позволяет наполнить
конкретным смыслом абстрактную философскую
формулу о том, что порядок, доведенный до крайней
сложности, переходит в хаос - свою диалектическую
противоположность. Так происходит, когда форма
поверхности настолько сложна, что в данном
масштабе рассмотрения выглядит как хаотическая
мозаика случайным образом раскрашенных
квадратиков (пикселов). Наиболее эффектного
результата можно добиться, если
экспериментировать с тригонометрическими
функциями. Они, будучи примененными к неким
несложным нелинейным выражениям, способны
порождать бесконечные, причудливо искривленные
волновые структуры. Ряды волн, все более
измельчающихся, превращаются на экране монитора
в особого рода завихрения - так называемые
муаровые эффекты. Если кому-то из читателей
повезет наткнуться в своих путешествиях по
нелинейному миру на что-то неординарное и
изысканное, возможно, этим стоит поделиться с
остальным человечеством. Присылайте найденные
вами функции. Я думаю, что наиболее интересные из
них вместе с именами первооткрывателей (вашими
именами) будут прославлены на страницах газеты.
Поэкспериментировав
с различными функциями, можно убедиться в том,
что простые нелинейные выражения нередко
определяют поверхности сложнейшей изысканной
формы. Мир математической нелинейности (как,
впрочем, и мир окружающей нас физической
реальности) неимоверно богат и разнообразен. Кто
знает, какие тайны еще скрыты в его глубинах.
Исследование функций двух переменных - крайне
занимательное занятие само по себе. Слегка
изменяя вид функции и масштаб картинки, можно
получить бесконечный ряд фантастически красивых
математических "пейзажей". Кроме того, такие
компьютерные экскурсии в мир математической
нелинейности весьма поучительны. Они развивают
способность иначе видеть окружающий нас мир и
гораздо глубже понимать его законы. Анализ
отдельных графиков позволяет наполнить
конкретным смыслом абстрактную философскую
формулу о том, что порядок, доведенный до крайней
сложности, переходит в хаос - свою диалектическую
противоположность. Так происходит, когда форма
поверхности настолько сложна, что в данном
масштабе рассмотрения выглядит как хаотическая
мозаика случайным образом раскрашенных
квадратиков (пикселов). Наиболее эффектного
результата можно добиться, если
экспериментировать с тригонометрическими
функциями. Они, будучи примененными к неким
несложным нелинейным выражениям, способны
порождать бесконечные, причудливо искривленные
волновые структуры. Ряды волн, все более
измельчающихся, превращаются на экране монитора
в особого рода завихрения - так называемые
муаровые эффекты. Если кому-то из читателей
повезет наткнуться в своих путешествиях по
нелинейному миру на что-то неординарное и
изысканное, возможно, этим стоит поделиться с
остальным человечеством. Присылайте найденные
вами функции. Я думаю, что наиболее интересные из
них вместе с именами первооткрывателей (вашими
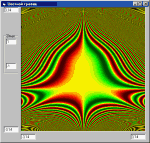
именами) будут прославлены на страницах газеты. В основу
программы построения кривых в полярных
координатах, приведенной на врезке, положено
циклическое изменение угла j. Для каждого нового
значения угла в подпрограмме-функции по заданной
формуле вычисляется значение r. В точке,
соответствующей заданному углу и вычисленной
длине полярного радиуса высвечивается пиксель
того или иного цвета. Наиболее эффектно выглядят
не единичные графики, а целые семейства кривых,
порождаемых выражениями с параметрами. Например,
фигура, приведенная на первом рисунке,
представляет собой семейство кривых, полученных
при помощи уравнения r=A(1+cos(3j)+B(sin(3j))2 (см.
книгу Котов Ю.В. Как рисует машина. - М.:Наука, 1988.).
Построение производилось путем варьирования
параметра А (параметр В принимал фиксированное
значение).
В основу
программы построения кривых в полярных
координатах, приведенной на врезке, положено
циклическое изменение угла j. Для каждого нового
значения угла в подпрограмме-функции по заданной
формуле вычисляется значение r. В точке,
соответствующей заданному углу и вычисленной
длине полярного радиуса высвечивается пиксель
того или иного цвета. Наиболее эффектно выглядят
не единичные графики, а целые семейства кривых,
порождаемых выражениями с параметрами. Например,
фигура, приведенная на первом рисунке,
представляет собой семейство кривых, полученных
при помощи уравнения r=A(1+cos(3j)+B(sin(3j))2 (см.
книгу Котов Ю.В. Как рисует машина. - М.:Наука, 1988.).
Построение производилось путем варьирования
параметра А (параметр В принимал фиксированное
значение).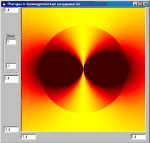 Варьируя
алгоритмы раскраски компьютерных изображений,
можно добиться впечатляющего сходства
математических кривых с реально существующими
живыми объектами, а можно, напротив, изобрести
что-то совершенно новое, но не менее прекрасное.
Получаешь истинное удовольствие, наблюдая за
тем, как в бархатной тьме экрана постепенно
появляется еле заметное темно-синее свечение,
которое постепенно распространяется от центра,
превращаясь в лепестки. По мере роста они
становятся сначала сиреневыми, затем ярко
красными, а по краям снова окрашиваются
темно-синим. Еще более разнообразные и
интересные изображения получаются в опытах с
цилиндрическими координатами. Здесь мы имеем
дело уже не с семейством кривых на плоскости, а с
объемными структурами. Например, вывернутый (в
цветном изображении золотой) диск на втором
рисунке представляет собой фрагмент графика
функции z = (cosfi ^ 2 / ro) ^ (Int(ro) + 1). В общем простор для
фантазии и экспериментов в этой области огромен.
Весьма незначительные усилия по разработке
несложного программного обеспечения сторицей
окупаются чрезвычайно эффектными результатами.
Попробуйте и убедитесь сами! Если в процессе
своих исследований наткнетесь на что-то
заслуживающее внимания - присылайте.
Варьируя
алгоритмы раскраски компьютерных изображений,
можно добиться впечатляющего сходства
математических кривых с реально существующими
живыми объектами, а можно, напротив, изобрести
что-то совершенно новое, но не менее прекрасное.
Получаешь истинное удовольствие, наблюдая за
тем, как в бархатной тьме экрана постепенно
появляется еле заметное темно-синее свечение,
которое постепенно распространяется от центра,
превращаясь в лепестки. По мере роста они
становятся сначала сиреневыми, затем ярко
красными, а по краям снова окрашиваются
темно-синим. Еще более разнообразные и
интересные изображения получаются в опытах с
цилиндрическими координатами. Здесь мы имеем
дело уже не с семейством кривых на плоскости, а с
объемными структурами. Например, вывернутый (в
цветном изображении золотой) диск на втором
рисунке представляет собой фрагмент графика
функции z = (cosfi ^ 2 / ro) ^ (Int(ro) + 1). В общем простор для
фантазии и экспериментов в этой области огромен.
Весьма незначительные усилия по разработке
несложного программного обеспечения сторицей
окупаются чрезвычайно эффектными результатами.
Попробуйте и убедитесь сами! Если в процессе
своих исследований наткнетесь на что-то
заслуживающее внимания - присылайте.