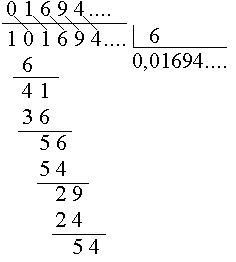Способность молниеносно производить в уме арифметические действия отнюдь не свидетельствует о высоком уровне общего развития и в еще меньшей степени о наличии математических способностей. Некоторые из выдающихся математиков не могли без ошибки подсчитать, какую сумму им надлежит получить сдачи при покупке какой-нибудь мелочи. В то же время многие профессиональные "чудо-вычислители" (хотя и не лучшие из них) во всем, что не касалось арифметических выкладок, были людьми весьма неразвитыми.

Тем не менее великие математики нередко отличались способностью мгновенно производить в уме сложнейшие расчеты. Например, Карл Фридрих Гаусс производил вычисления с такой быстротой и так искусно, что ему мог бы позавидовать любой эстрадный вычислитель. Не без тщеславия он любил говорить о себе, что научился вычислять раньше, чем говорить". Как-то раз отец Гаусса, бравший подряды на строительные работы, подсчитывал, сколько он должен уплатить своим каменщикам за неделю. Трехлетний Фридрих озадачил отца, сказав:

— Папа, ты ошибся...

Мальчик назвал число, которое действительно оказалось правильным, хотя установить это удалось лишь после кропотливой проверки. Самым удивительным было то, что никто не учил малолетнего ревизора арифметике.

Джон фон Нейман был разносторонним математическим гением, обладавшим способностью производить сложнейшие вычисления, не прибегая к карандашу и бумаге. В своей книге "Ярче тысячи солнц" Р. Юнг (цитируя другого ученого) описывает следующий случай. "Однажды в кабинете Теллера собрались Ферми, фон Нейман и Фейнман. Я также присутствовал, так как мне предстояло выполнять планируемые здесь вычисления. Возникало и отвергалось много разных идей, и через каждые несколько минут у Ферми и Теллера появлялась необходимость быстрой численной проверки. И тогда ученые начинали действовать: Фейнман с помощью настольного арифмометра, Ферми с помощью маленькой логарифмической линейки, которую постоянно носил с собой, а фон Нейман обходился собственной головой. Голова обычно срабатывала быстрее, и было поразительно, как близко совпадали все три ответа".

Способность к устному счету таких первоклассных математиков, как Гаусс, фон Нейман, Эйлер или Валлис, не может не вызывать восхищения. Однако все их достижения в этой области меркнут по сравнению с чудесами, которые демонстрировали на эстраде профессиональные "чудо-вычислители". Многочисленные представители того племени акробатов и жонглеров ума с успехом подвизались в прошлом веке на подмостках Англии, континентальной Европы и Америки. Многие из них начинали свои выступления, еще будучи маленькими детьми. И хотя некоторые из вычислителей писали о своих методах и подвергались обследованию в лабораториях психологов, большую часть своих секретов они, по-видимому, утаивали или, скорее всего, сами до конца не понимали, каким образом им удается делать то, что они делают.

Первый из американских эстрадных вычислителей Зepa Колберн родился в 1804 г. в Кэботе (штат Вермонт). Так же как у его отца, прабабушки и по крайней мере у одного из братьев, у Зера было по шесть пальцев нa каждой руке и ноге. ("Лишние" пальцы были ампутированы, когда Зера исполнилось 10 лет. Как знать, может быть, именно они способствовали пробуждениюу Зера интереса к счету и вычислениям?) Таблицу умножения всех чисел до 100 он выучил задолго до того, как научился писать и читать. Отец Зера, бедный фермер, быстро понял, какое золотое дно таят в себе необычайные способности сына, и, когда Зера исполнилось всего лишь 6 лет, отправился с ним в первое турне. В возрасте 8 лет Колберн выступал в Англии. Сохранились официальные протоколы его выступлений. Он мог почти мгновенно умножать одно на другое два четырехзначных числа и задумался лишь на миг, когда ему предложили перемножить два пятизначных числа. Когда Колберна попросили умножить 21734 на 543, он тотчас же назвал ответ: 11801562. На вопрос, каким образом ему это удалось, Колберн ответил, что 543 - это 3 x 181. Поскольку умножать на 181 легче, чем на 543, он сначала умножил 21734 на 3, а полученный результат умножил на 181.

Вашингтон Ирвинг и другие поклонники необыкновенного таланта мальчика собрали достаточную сумму денег, чтобы отправить юного Колберна в школу сначала в Париже, а затем в Лондоне. Что произошло дальше, доподлинно не известно: то ли вычислительные способности Колберна ослабели, то ли он просто потерял интерес к выступлениям на эстраде. По возвращении в Америку (ему тогда было 20 лет) он в течение 10 лет служил священником методистской церкви. Его необычайная автобиография была опубликована в 1833 г. под названием "Воспоминания Зера Колберна, написанные им самим,... с изложением оригинальных методов вычислений". Колберн умер в возрасте 35 лет, будучи преподавателем иностранных языков в Норвичском университете (г. Нортфилд, штат Вермонт).

Английским соперником Колберна был Джордж Паркер Биддер, родившийся в 1806 г. в Девоншире. По преданию, отец Биддера, по профессии каменщик, научил сына лишь считать. Арифметику Биддер "открыл" самостоятельно, играя шариками и пуговицами. Когда ему исполнилось 9 лет, он в сопровождении отца отправился в свою первую гастрольную поездку. Типичным среди вопросов, которые задавали ему любопытные, был, например, такой: "Если Луна находится на расстоянии 123256 миль от Земли, а звук распространяется со скоростью 4 мили в минуту, то сколько времени потрется звуку, чтобы пройти путь от Земли до Луны предположении, что звук может распространяться в безвоздушном пространстве)?" Менее чем через минуту мальчик ответил: "21 сутки 9 часов 34 минуты". Как-то раз, когда Биддеру было 10 лет, его попросили извлечь квадратный корень из 119550669121. Результат был получен через 30 секунд: 345761. В 1818 г., когда Биддеру было 12, а Колберну 14 лет, оба вундеркинда встретились в Дербишире и вступили в состязание друг с другом. В своих мемуарах Колберн утверждает, что победа досталась ему, но лондонские газеты того времени отдают пальму первенства Биддеру.

Профессора Эдинбургского университета убедили Биддера-старшего предоставить им право позаботиться об образовании сына. Мальчик с успехом окончил колледж и впоследствии стал одним из лучших инженеров Англии. В основном ему приходилось заниматься строительством железных дорог, но наибольшую известность он снискал как автор проекта и руководитель постройки доков Виктории в Лондоне. С возрастом Биддер не утратил способности производить в уме головоломнейшие выкладки. Незадолго до его смерти, последовавшей в 1878 г., кто-то, упомянув, что в одном дюйме укладывается 36.918 длин волн красного света и что свет распространяется со скоростью 190.000 миль в секунду, поинтересовался, сколько волн красного света успевает достичь сетчатой оболочки глаза в течение одной секунды. "Не трудитесь считать, - ответил Биддер, - 444.443.651.200.000".

236 х 47 236 = 200 + 30 + 6 47 = 40 + 7 1. 40 х 200 = 8.000 2. 8.000 + (40 х 30) = 9.200 3. 9.200 + (40 x 6) = 9.440 4. 9.440 + (7 x 200) = 10.840 5. 10.840 + (7 x 30) = 11.050 6. 11.050 + (7 x 6) = 11.092   Рис. 151. Вычисление произведений   методом Зера Колберна.

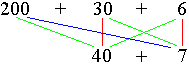
И Колберн, и Биддер вычисляли произведения больших чисел, разбивая их на части и умножая слева направо "перекрестным методом". Например, вычисляя произведение 236 x 47, Колберн сначала разбивал сомножители на части - (200 + 30 + 6) x (40 + 7), - а затем дейcтвовал так, как показано на рис. 151. Попробуйте, закрыв глаза, вычислить какое-нибудь произведение по методу Колберна и вы убедитесь, что он позволяет производить вычисления в уме гораздо легче, чем обычный способ умножения справа налево. "Правда, этот метод... требует использования гораздо большего количества чисел, чем обычные правила, - пишет Колберн в своих мемуарах, — но не следует упускать из виду, что перья, чернила и бумага обходились Зера весьма дешево". (В своей книге Колберн говорит о себе в третьем лице.) Почему производить вычисления в уме с помощью "перекрестного метода" легче, чем по обычным правилам? Выступая в лондонском Институте гражданских инженеров с лекцией о своих методах вычислений, Биддер так ответил на этот вопрос: "На каждом этапе метод позволяет иметь дело с одним и только с одним фактом. Лишь его необходимо удерживать в памяти до тех пор, пока очередной этап вычислений не будет завершен".

Другая причина, по которой эстрадные вычислители предпочитают умножать числа слева направо (хотя они редко признаются в этом), заключается в том, что, умножая слева направо, они получают возможность называть цифры произведения до того, как вычисление его будет закончено. Эстрадные вычислители прибегают и к другим уловкам, чтобы создать у зрителей впечатление, будто время, затрачиваемое ими на получение ответа, меньше того, которое они затрачивают в действительности. Так, например, они повторяют вопрос, а затем отвечают так, будто результат мгновенно пришел им в голову, хотя вычислять ответ они начинают еще до того, как зритель успевает назвать последнюю цифру второго сомножителя. Иногда вычислитель выигрывает еще немного времени, притворившись, будто не расслышал вопроса, и попросив повторить его еще раз, Читая сообщения очевидцев о "мгновенных" вычислениях, производимых тем или иным чудесником на эстраде, всегда надлежит вводить поправку на подобные "отвлекающие маневры".

Так называемые вычислители-"идиоты" не представляют особого интереса, и я упомяну лишь одного из них. Должен заметить, что все они отнюдь не были столь безнадежными идиотами, как считала публика. Кроме того, они значительно уступали эстрадным вычислителям с более развитым интеллектом по скорости, с которой производили арифметические действия.

Одним из первых представителей "умственно неполноценных" вычислителей был английский фермер Джедедия Бакстон, живший в XVIII в. Всю свою жизнь он был фермером и никогда не выступал перед публикой. Тем не менее слух о его необыкновенных способностях распространился по округе и достиг Лондона, куда Бакстон был вызван, дабы члены Королевского общества могли убедиться в том, что имеют дело с "чудом природы". Во время пребывания Бакстона в Лондоне кто-то вздумал пригласить его в Друрилейнский театр на трагедию Шекспира "Ричард III" с прославленным актером Дэвидом Гарриком в главной роли. На вопрос о том, как ему понравился спектакль, Бакстон ответил, что Гаррик произнес 14445 слов и сделал 5202 шага по сцене. У Бакстона была непреодолимая страсть подсчитывать и измерять решительно все, что попадалось ему на глаза. Рассказывают, что, пройдя по полю, он мог с необычайной точностью назвать его площадь в квадратных дюймах и тут же перевести их в... "квадратные толщины волоса" (из расчета 48 волос в одном дюйме). Бакстон никогда не учился и не умел читать, писать и обращаться с цифрами.

Примером вычислителей с высокоразвитыми умственными способностями может служить профессор математики Эддибургского университета Александр Крейг Эйткен. Он родился в 1895 г. в Новой Зеландии. В отличие от большинства людей, способных "молниеносно" производить в уме вычисления, Эйткен ничем не проявлял своего дарования до 13 лет. Впрочем, и в этом возрасте его интерес пробудился в основном к алгебре, а не к арифметике.

В 1954 г., почти через сто лет после исторической лекции Биддера, Эйткен выступил перед лондонским Обществом инженеров с докладом на тему "Искусство устного счета (доклад сопровождается демонстрацией различных приемов устного счета)". Доклад Эйткена - это авторитетный отчет о том, что происходит в уме человека, способного, не прикасаясь к карандашу и бумаге, быстро производить сложнейшие вычисления, отчет тем более ценный, что исходит от человека, наделенного такой способностью.

Совершенно необходимой предпосылкой к деятельности "чудо-вычислителя" служит врожденная способность быстро запоминать числа. Все выдающиеся вычислители обладали этой способностью и нередко демонстрировали ее в своих выступлениях. Десятилетний Биддер с легкостью называл по порядку все цифры 40-значного числа, которые зрители по его просьбе сообщали ему в обратном порядке. Многие эстрадные вычислители, заканчивая свое выступление, могли безошибочно называть все "участвовавшие" в нем числа.

Существуют различные мнемонические приемы, позволяющие заменять числа словами, которые поддаются запоминанию с помощью других мнемонических приемов, однако все они слишком медленны для того, чтобы ими можно было пользоваться на сцене, и мастера-вычислители ими, несомненно, не пользовались. "Я никогда не прибегал к мнемоническим приемам, - заявил в своем докладе Эйткен, - и отношусь к ним с глубоким недоверием. Они лишь отягощают случайными и не относящимися к делу ассоциациями способность, которая должна проявляться в чистом, незамутненном виде".

Здесь же Эйткен упомянул об одном забавном случае, о котором он прочитал в газетах. Современного французского эстрадного вычислителя Мориса Дагбера обвинили в "бессмысленной трате времени и энергии", когда он запомнил 707 знаков десятичного разложения числа pi, полученного в 1873 г. Вильямом Шенксом. "Мне было приятно сознавать, - сказал Эйткен, - что я проделал это за несколько лет до Дагбера и не встретил никаких трудностей. Мне пришлось лишь разбить знаки нa строки по 50 цифр в каждой строке, затем каждые 50 цифр разбить на 10 групп по 5 цифр, а затем прочитать эти пятерки с соблюдением определенного ритма, как стихотворение. Запоминание 707 знаков, полученных Шенксом, было бы абсолютно бессмысленным занятием, если бы оно не было так просто".

Через 20 лет после того, как современные ЭВМ позволили вычислить pi с точностью до нескольких тысяч знаков, Эйткен узнал, что несчастный Шенкс ошибся в своих вычислениях и последние 180 знаков привел неверно. "Мне доставило удовольствие, - продолжал Эйткен, - выучить правильное значение pi до 1000-го знака. И снова я не встретил никаких трудностей. Единственное, что потребовалось, - это "сшить" уже хранившиеся в моей памяти цифры с новыми там, где Шенкс допустил ошибку. Я считаю, что секрет успеха заключается в умении расслабляться, в полной антитезе умению сосредоточиться. Важную роль играет заинтересованность. Случайная последовательность чисел, не представляющих никакого интереса с точки зрения математики, производила бы на меня отталкивающее впечатление. Если бы мне потребовалось запомнить их, я бы, разумеется, смог это сделать, но не без внутреннего сопротивления".

Здесь Эйткен прервал свою лекцию, чтобы привести на память (с явным соблюдением ритма) 250 знаков десятичного разложения pi. Кто-то из присутствующих попросил его продолжить "чтение" десятичного разложения pi с 301-го знака. После того как Эйткен назвал 50 знаков, его попросили перейти сразу к 501-му знаку, что он и сделал, назвав еще 150 знаков. Все цифры были названы без единой ошибки (присутствовавшие проверяли правильность называемых Эйткеном знаков по таблице).

Используют ли эстрадные вычислители, манипулируя числами, свое "внутреннее зрение", "видят" ли они мысленно те числа, с которыми работают? Единого ответа на этот вопрос дать нельзя. Некоторые вычислители представляют числа написанными на доске или на листе бумаги, другие предпочитают воспринимать числа на слух, третьи просто не в состоянии объяснить, как они работают. Французский психолог Альфред Бине входил в состав комитета, созданного в конце прошлого века Французской Академией наук для изучения процесса мышления двух выдающихся эстрадных вычислителей - грека, Перикола Диаманди и итальянца Жака Инауди! В выпущенной в 1894 г. книге "Психология выдающихся вычислителей и мастеров игры в шашки" Бине сообщал, что Диаманди мысленно представлял себе доску с написанными на ней числами, с которыми он производил различные действия, а Инауди, производивший арифметические выкладки в 6 раз быстрее, был вычислителем аудиоритмического типа. Вычислители визуального типа, хотя к их числу принадлежат столь выдающиеся мастера, как Дагбер, польский вычислитель Сало Финкельштейн и замечательная французская вычислительница, выступавшая под псевдонимом мадмуазель Осака, обычно работают медленнее своих собратьев по профессии, которым не требуется "видеть" числа. Например, такие вычислители аудиотипа, как Биддер, работали явно быстрее. По-видимому, рекорд быстроты принадлежит ныне здравствующему голландскому эстрадному вычислителю Вильяму Клейну, который выступает под псевдонимом Паскаль. Он способен перемножить 2 десятизначных числа менее чем за 2 минуты. Клейн также принадлежит к аудиотипу. Более того, он просто не в состоянии производить вычисления, не бормоча себе при этом под нос. Если Клейн ошибается, то это обычно связано с тем, что он путает два близких по звучанию числа.

В своем докладе Эйткен утверждал, что он по желанию может мысленно представить себе числа написанными на бумаге. На различных этапах вычислений и в особенности на завершающем этапе числа могут самопроизвольно возникать перед мысленным взором вычислителя. "Но в основном они как бы прячутся под неким покровом, продолжая двигаться в скрытом состоянии и перестраиваться в нужном порядке с неукоснительной точностью. В частности, я могу со всей определенностью утверждать, что лишние нули в начале или в конце числа никогда не возникают перед моим мысленным взором на промежуточных этапах вычислений. Выражение "перед мысленным взором" здесь не совсем точно. Речь идет не о способности видеть или слышать, а о некоторой более общей способности, объединяющей черты той и другой, адекватное описание которой мне не приходилось встречать в литературе (как, впрочем, не приходилось встречать и адекватного описания мыслительных процессов, обусловливающих музыкальную память или способность сочинять музыку). Не могу не отметить также, что в некоторых случаях разум опережает волю: я получаю ответ до того, как у меня возникает желание произвести вычисления. Я неоднократно проверял это и, к своему удивлению, всегда обнаруживал, что такой предугаданный ответ верен".

Эйткен умудряется хранить в своей памяти поистине чудовищное количество разнообразнейших сведений. Высокая "информационная емкость" характерна для всех эстрадных вычислителей. Вряд ли найдется хоть один из них, кто не знал бы таблицу умножения до 100 x 100, а специалисты утверждают, что Биддер и некоторые другие вычислители удерживали в памяти, хотя и бессознательно, таблицу умножения до 1000 x 1000. (Числа, превышающие 1000, эстрадные вычислители перемножают, разбивая их на пары и тройки цифр, с которыми можно обращаться, как с отдельными цифрами.) В памяти эстрадного вычислителя хранятся обширные таблицы квадратов, кубов, логарифмов, а также множество других числовых данных, полезных при ответах на вопросы, задаваемые аудиторией, например число секунд в году или унций в тонне. Поскольку 97 - наибольшее из простых чисел, не превышающих 100, к эстрадным вычислителям часто обращаются с просьбой назвать 96-значный период десятичного разложения дроби 1/97. Эйткен давно запомнил этот период и, если кому-либо из присутствующих на его выступлении приходит в голову поинтересоваться бесконечной периодической дробью 1/97, выпаливает все 96 знаков периода без малейшей задержки.

Помимо природных данных, существуют сотни способов ускорить вычисления, которые эстрадный вычислитель либо выучивает, либо изобретает. Как отметил в своем докладе Эйткен, первое, с чего приходится начинать любое вычисление - это выбор в мгновение ока оптимальной стратегии вычислений. В качестве примера Эйткен раскрыл один удивительный и не слишком известный секрет вычислителей. Предположим, вас попросили перевести в десятичную дробь 1/k, где целое число k заканчивается девяткой (например, k = 59). Вместо того, чтобы делить 1 на 59, вы можете прибавить 1 к 59, превратив тем самым 59 в 60, после чего разделить 0,1 на 6 так, как показано на рис. 152. (Метод Эйткена сводится к последовательной корректировке делимого: получив в частном очередную цифру, он вводит ее в делимое с "опозданием" на один знак. Для удобства сравнения частное повторено над делимым.)

"Представим теперь, - продолжает Эйткен, - что вас попросили перевести в десятичную дробь 5/23. Я сразу вижу, что, умножив числитель и знаменатель дроби на 3, получу эквивалентную дробь 15/69, знаменатель которой заканчивается весьма удобной девяткой". Перед вычислителем возникает дилемма: "превратить" 69 в 70 и разделить 1,5 на 7 по только что описанному способу или же, умножив числитель и знаменатель исходной дроби на 13, превратить ее в 65/299 и разделить затем 0,65 на 3 (при этом цифры из частного в корректируемый делитель будут попадать с "опозданием" на два знака).

Какая стратегия лучше? "Решение, - говорит Эйткен, - следует принимать, не колеблясь ни минуты, и, избрав стратегию раз и навсегда, неукоснительно идти к цели. Посреди вычислений в голову может прийти мысль о том, что другая стратегия лучше. Даже если это так, запоздалое озарение следует безжалостно отбросить и продолжать скачки на лошади, даже явно уступающей по своим достоинствам более резвому скакуну".

Ниже показано, как Эйткен возводит в квадрат число 777.

Задача: 777 x 777 = ?

a² = [(a + b) x (a - b)] + b²,

777² = [(777 + 23) x (777 - 23)] + 23,

777² = [800 x 754] + 529,

777² = 603.200 + 529,

777² = 603.729.

Число b выбирается так, чтобы оно было по возможности меньше и чтобы одно из чисел (а + b) или (а - b) заканчивалось как можно более длинной цепочкой нулей. В данном случае Эйткен выбрал b = 23. Помня таблицу квадратов небольших чисел, он, не задумываясь, возводит 23 в квадрат, получая 529. Во время доклада Эйткен привел 7 трехзначных чисел, которые тут же возвел в квадрат.

Удительно простое правило возведения в квадрат двузначных чисел, оканчивающихся на 5, непосредственно вытекает из метода Эйткена. Оно так просто, что заслуживает, чтобы его запомнить: первую цифру числа нужно умножить на нее же плюс единица, а к полученному произведению справа приписать 25. Пусть, например, требуется возвести в квадрат 85. Умножая 8 на (8 + 1) = 9, получаем 72. Приписывая справа 25, находим окончательный ответ: 85 x 85 = 7225.

Рис. 152. Перевод 1/59 в     десятичную дробь методом   Эйткена.

Математик из Глазго Томас О'Бейрн рассказывает о том, как однажды он вместе с Эйткеном отправился на выставку-распродажу настольных вычислительных машин. "Коммивояжер, демонстрировавший машины, произнес нечто вроде:

- А сейчас мы умножим: 23586 на 71283... Стоявший рядом Эйткен тотчас же продолжил:

- ... и получим столько-то.

Ответ был совершенно правильным. Коммивояжер был слишком поглощен стремлением продать машину и ничего не заметил, но наблюдавший сцену представитель фирмы, убедившись, что Эйткен не ошибся, чуть не упал в обморок. Я тоже".

В наши дни бурное развитие вычислительной техники не поощряет молодых людей, обладающих выраженными способностями к устному счету, совершенствовать свое искусство. В заключение своего доклада Эйткен признал, что и его способности к молниеносному счету стали слабеть после того, как он познакомился с первым арифмометром и убедился, каким бесполезным становится его искусство. "Люди, способные производить в уме сложнейшие выкладки, по-видимому, обречены на вымирание, подобно аборигенам Тасмании или маорийцам, - с горечью заметил он. - Поэтому вы можете испытывать интерес, близкий к тому, какой испытывают антропологи, наблюдая любопытный образчик исчезающего племени вычислителей. Может быть, кто-нибудь из моих слушателей, дожив до 2000 г., сможет с гордостью сказать:

- Да, одного такого я знал".